

問題
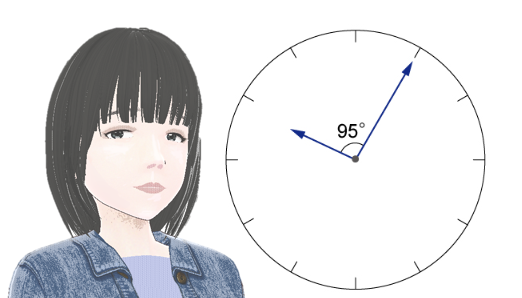
時計を見たとき、図のように長針はちょうど文字盤の目盛りをさしていて、長針と短針のなす角が95度になっています。
さて現在の時刻は何時何分ですか。ただし、この時計は「12」の目もりの位置が分かりません。
問題文を翻訳してみる
翻訳というと英語などの外国語から日本語へというイメージがあるかもしれませんが、ここでいう翻訳は、複雑な問題文や難解な問題文、あるいは解きにくい形の問題文を、わかりやすく解きやすい形の文章に変えるということになります。
この問題を別の言い方で考えてみると、次のように言い換えることができます。

正確な時計があります。
今、長針がちょうど文字盤の目盛りを指していて、かつ長針と短針がつくる角度が95度になっています。
さて、今この時間は、何時何分でしょうか?
問題の解法と予備知識
この問題の解答方法はいくつかあります。
そのうちの一つをご紹介します。
まずは、この問題を解くにあたり最低限必要な知識は、短針と長針が単位時間に動く距離(角度)です。
知識としては、「長針は1分間に6°、短針は1分間に0.5°動く」という知識が必要ですが、これは暗記する必要なんてありません。
長針は1時間で時計の文字盤を1周する、つまり360°動くわけですので、1分間では、360°÷60分=6°/分動きます。
短針は、12時間で文字盤を1周するので、1時間では360°÷12時間=30°/時動きますので、分になおせば、1時間は60分なので、1分間では30°÷60分=0.5°/分動くことがわかります。
制限されたもの(長針)から攻めていく
この問題で、長針は文字盤の丁度目盛りと重なっているということなので、時計の文字盤の1~12までのところのいずれかにあるので、12ケースの可能性しかありません。
12ケースについて、12時(0時)のところを0°として、角度を出してみます。
すると、長針がある位置は、文字盤の目盛りと一致するので、12時のところから数えて、30°、60°、90°というように、30°ずつ増えた角度の位置にあることがわかります。
次に、短針は長針と95°ズレた位置にあるので、12のケースについてそれぞれ、時計回りに95°ズレた位置にある場合と、反時計回りに95°ズレた位置にある場合があります。
その角度を一覧表を作り書き込みます。
計算は、30°ずつずらしていけばいいだけなので簡単です。
| 文字盤 | 長針時間 | 長針の位置 | プラス95° | マイナス95° |
|---|---|---|---|---|
| 12 | 0分 | 0° | 95° | 265° |
| 1 | 5分 | 30° | 125° | 295° |
| 2 | 10分 | 60° | 155° | 325° |
| 3 | 15分 | 90° | 185° | 355° |
| 4 | 20分 | 120° | 215° | 25° |
| 5 | 25分 | 150° | 245° | 55° |
| 6 | 30分 | 180° | 275° | 85° |
| 7 | 35分 | 210° | 305° | 115° |
| 8 | 40分 | 240° | 335° | 145° |
| 9 | 45分 | 270° | 5° | 175° |
| 10 | 50分 | 300° | 35° | 205° |
| 11 | 55分 | 330° | 65° | 235° |
短針が取り得る位置を検討する
長針が文字盤のいずれかの目盛りの位置にあるとき、短針が取り得る位置を検討します。
つまり、毎時0分、5分、10分、15分、20分、25分、30分、35分、40分、45分、50分、55分のとき、短針は1分に0.5°動くので、それぞれの文字盤の目盛りがらう位置からそれぞれ、0°、2.5°、5°、7.5°、10°、12.5°、15°、17.5°、20°、22.5°、25°、27.5°進んだ位置にあることになります。
長針は、角度として30の倍数になる位置にあり、そこから短針は95°ズレた位置にあることから、短針がある位置の角度の一の位は、5である必要があります。
つまり、可能性としては、長針が10分、30分、50分の位置にあるケースのみにしぼられます。
| 文字盤 | 長針時間 | 長針の位置 | プラス95° | マイナス95° | 短針(文字盤+) |
|---|---|---|---|---|---|
| 12 | 0分 | 0° | 95° | 265° | 0° |
| 1 | 5分 | 30° | 125° | 295° | 2.5° |
| 2 | 10分 | 60° | 155° | 325° | 5° |
| 3 | 15分 | 90° | 185° | 355° | 7.5° |
| 4 | 20分 | 120° | 215° | 25° | 10° |
| 5 | 25分 | 150° | 245° | 55° | 12.5° |
| 6 | 30分 | 180° | 275° | 85° | 15° |
| 7 | 35分 | 210° | 305° | 115° | 17.5° |
| 8 | 40分 | 240° | 335° | 145° | 20° |
| 9 | 45分 | 270° | 5° | 175° | 22.5° |
| 10 | 50分 | 300° | 35° | 205° | 25° |
| 11 | 55分 | 330° | 65° | 235° | 27.5° |
それぞれのケースを検証
〇時10分とした場合、長針は60°の位置にあり、短針は155°の位置か325°の位置にあるはずです。
長針が10分の位置なので、短針は文字盤の目盛りから5°進んだところにあるため、5°を引きます。
155-5=150となり、ちょうど30の倍数の150°になります。
つまり、短針は150°(5時の位置)から10分進んだ位置にあることがわかるので、5時10分に長針と短針の角度が95°になることがわかります。
同様にして、325-5=320となりますが、30の倍数でないので、ちょうど95°にはならないことがわかります。
〇時30分とした場合、長針は180°の位置にあり、短針は275°の位置か85°の位置にあるはずです。
長針が30分の位置なので、短針は文字盤の目盛りから15°進んだところにあるため、15°を引きます。
275-15=260、85-15=70となり、30の倍数でないので、ちょうど95°にはならないことがわかります。
〇時50分とした場合、長針は300°の位置にあり、短針は35°の位置か205°の位置にあるはずです。
長針が50分の位置なので、短針は文字盤の目盛りから25°進んだところにあるため、25°を引きます。
35-25=10は、30の倍数でないので、ちょうど95°にはならないことがわかります。
一方、205-25=180となり、30の倍数になります。
つまり、短針は180°(6時の位置)から50分進んだ位置にあることがわかるので、6時50分に長針と短針の角度が95°になることがわかります。
したがって、長針と短針の角度が95°になる時間は2つあり、5時10分と、6時50分になります。