電球スイッチＯＮ・ＯＦＦ問題

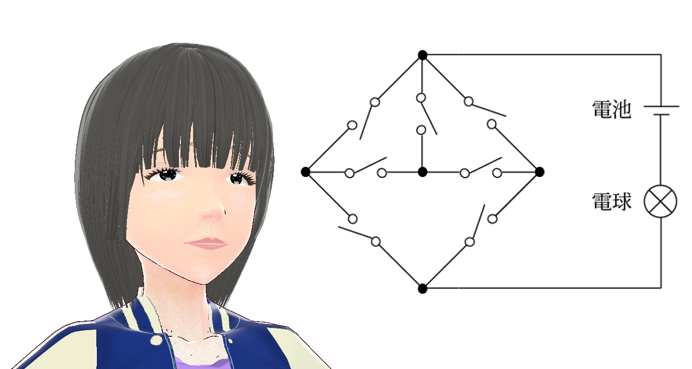
図のような、電池１個、電球１個、スイッチ７個を含む電気回路があります。
スイッチのオン・オフの仕方は全部で１２８通りあり、そのうち電球が点灯するようなスイツチのオン・オフの仕方は全部で何通りあるでしょうか。

まずは、それぞれのスイッチを図のようにＡ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇとナンバーリングします。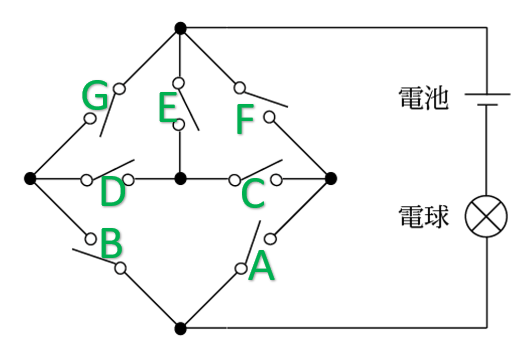

Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇのうち、ＯＮのスイッチが０か１の場合は電球は点灯しない。

ＯＮのスイッチが２つの場合は、ＡとＦ、ＢとＧの組み合わせのみ点灯します。
したがって、ＯＮのスイッチが２つの場合は、電球が点灯する組み合わせは２通りあります。

ＯＮのスイッチが３つの場合は、ＡとＣとＥ、ＢとＤとＥの組み合わせの時に点灯します。
さらにＡとＦとそれ以外のどれか１つ、ＢとＧとそれ以外のどれか１つの場合も点灯します。
このケースの場合、残りの５つのうちどれでもいいので、それぞれ５通りずつあります。
したがって、ＯＮのスイッチが３つの場合は、電球が点灯する組み合わせは、２＋５＋５＝１２通りあります。

ＯＮのスイッチが４つの場合は、ＡとＣとＤとＧ、ＢとＤとＣとＦの組み合わせの時に点灯します。
さらにＡとＦとそれ以外のどれか２つ、ＢとＧとそれ以外のどれか２つの場合も点灯します。
このケースの場合は、残りの４つのうちから２つ選ぶ組み合わせなので、（４×３）／（２×１）＝６通りずつあります。
しかし、ここには罠があります。
ＡとＦ以外にＢとＧがＯＮになっている場合と、ＢとＧ以外にＡとＦがＯＮになっている場合は、重複して数えられていることになるので、この分は差し引いて考えなければいけません。
さらにＡとＣとＥとそれ以外のどれか１つ、ＢとＤとＥとそれ以外のどれか１つの場合も点灯します。
このケースの場合は、残りの４つのうちどれでもいいので、それぞれ４通りずつあります。
したがって、ＯＮのスイッチが４つの場合は、電球が点灯する組み合わせは、２＋６＋６＋４＋４－１＝２１通りあります。

ＯＮのスイッチが５つの場合は、ＯＦＦになっているのが２つということになるので、ＯＦＦになった残りの２つがＡとＢである場合以外は、すべて電球は点灯します。
したがって、７つから５つを選ぶ方法は、（７×６×５×４×３）／（５×４×３×２×１）＝２１通りとなり、先ほどのＡとＢ以外、つまりＣ、Ｄ、Ｅ、Ｆ、ＧがＯＮになっているケースを差し引くので、２１－１＝２０通りあります。

ＯＮのスイッチが６つの場合は、全て電球は点灯します。
この組み合わせは、ＯＦＦになっているスイッチが１つと逆に考えれば、７通りということがすぐにわかります。

ＯＮのスイッチが７つの場合は、もちろん電球は点灯し、これは当たり前ですが１通りです。

つまり、ＯＮのスイッチが０または１つの場合は０通り、２つの場合は２通り、３つの場合は１２通り、４つの場合は２１通り、５つの場合は２０通り、６つの場合は７通り、７つの場合は１通りとなりますので、０＋０＋２＋１２＋２１＋２０＋７＋１＝６３通りということになります。